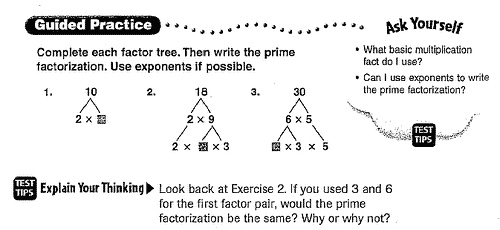
Mr Person at Text Savvy looks at an example of ‘Guided Practice’ in a maths textbook – the ‘guidance’ actually requiring attention from the teacher before the students can move on to working independently – and asks whether some type of architecture of control (a forcing function perhaps) would improve the situation, by making sure (to some extent) that each student understood what’s going on before being able to continue:
Image from Text Savvy
Is there room here for an architecture of control, which can make Guided Practice live up to its name?
This is a very interesting problem. Of course, learning software could prevent the student moving to the next screen until the correct answer is entered in a box. This must have been done hundreds of times in educational software, perhaps combined with tooltips (or the equivalent) that explain what the error is, or how to think differently to solve it – something like the following (I’ve just mocked this up, apologies for the hideous design):
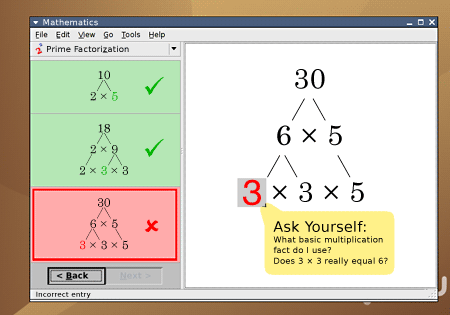
The ‘Next’ button is greyed out to prevent the student advancing to the next problem until this one is correctly solved, and the deformed speech bubble thing gives a hint on how to think about correcting the error.
But just as a teacher doesn’t know absolutely if a student has really worked out the answer for him/herself, or copied it from another student, or guessed it, so the software doesn’t ‘know’ that the student has really solved the problem in the ‘correct’ way. (Certainly in my mock-up above, it wouldn’t be too difficult to guess the answer without having any understanding of the principle involved. We might say, “Well, implement a ‘3 wrong answers and you’re out’ policy to stop guessing,” but how does that actually help the student learn? I’ll return to this point later.)
Blind spots in understanding
I think that brings us to something which, frankly, worried me a lot when I was a kid, and still intrigues (and scares) me today: no-one can ever really know how (or how well) someone else ‘understands’ something.
What do I mean by that?
I think we all, if we’re honest, will admit to having areas of knowledge / expertise / understanding on which we’re woolly, ignorant, or with which we are not fully at ease. Sometimes the lack of knowledge actually scares us; other times it’s merely embarrassing.
For many people, maths (anything beyond simple arithmetic) is something to be feared. For others, it’s practical stuff such as car maintenance, household wiring, and so on. Medicine and medical stuff worries me, because I have never made the effort to learn enough about it, and it’s something that could affect me in a major way; equally, I’m pretty ignorant of a lot of literature, poetry and fine art, but that’s embarrassing rather than worrying.
Think for yourself: which areas of knowledge are outside your domain, and does your lack of understanding scare/intimidate you, or just embarrass you? Or don’t you mind either way?
Bringing this back to education, think back to exams, tests and other assessments you’ve taken in your life. How much did you “get away with”? Be honest. How many aspects did you fail to understand, yet still get away without confronting? In some universities in the UK, for instance, the pass mark for exams and courses is 40%. That may be an extreme, and it doesn’t necessarily follow that some students actually fail to understand 60% of what they’re taught and still pass, but it does mean that a lot of people are ‘qualified’ without fully understanding aspects of their own subject.
What’s also important is that even if everyone in the class got, say, 75% right, that 75% understanding would be different for each person: if we had four questions, A, B, C and D, some people would get A, B, and C right and D wrong; others A, B, D right and C wrong, and so on. Overall, the ‘understanding in common’ among a sample of students would be nowhere near 75%. It might, in fact, be small. And even if two students have both got the same answer right, they may ‘understand’ the issue differently, and may not be able to understand how the other one understands it. How does a teacher cope with this? How can a textbook handle it? How should assessors handle it?
I’ll admit something here. I never ‘liked’ algebraic factorisation when I was doing GCSE (age 14-15) A-level (16-17) or engineering degree level maths – I could work out that, say, (2x² + 2)(3x + 5)(x – 1) = 6x^4 + 4x³ – 4x² + 4x – 10 (I think! I don’t think there’s an HTML character code for a superscript 4, sorry), but there’s no way I could have done that in reverse, extracting the factors (2x² + 2)(3x + 5)(x – 1) from the expanded expression, other than by laborious trial and error. Something in my mathematical understanding made me ‘unable’ to do this, but I still got away with it, and other than meaning I wasted a bit more time in exams, I don’t think this blind spot affected me too much.
OK, that’s an excessively boring example, but there must be many much, much worse examples where an understanding blind spot has actually adversely affected a situation, or the competence of a whole company or project. Just reading sites such as Ben Goldacre’s Bad Science (where some shocking scientific misunderstandings and nonsense are highlighted) or even SharkTank (where some dreadful IT misunderstandings, often by management, are chronicled) or any number of other collections of failures, shows very clearly that there are a lot of people in influential positions, with great power and resources at their fingertips, who have significant knowledge and understanding blind spots even within domains with which they are supposedly professionally involved.
Forcing functions in textbooks
Back to education again, then: assuming that we agree that incompetence is bad, then gaps in understanding are important to resolve, or at least to investigate. How well can a teaching system or textbook be designed to make sure students really understand what they’re doing?
Putting mistake-proofing (poka-yoke) or forcing functions into conventional paper textbooks is much harder than doing it in software, but there are ways of doing it. A few years ago, I remember coming across a couple of late-1960s SI Metric training manuals which claimed to be able to “convert” the way the reader thought (i.e. Imperial to SI) through a “unique” method, which was quoted on the cover (in rather direct language) as something like “You make a mistake: you are CORRECTED. You fail to grasp a fundamental concept: you CANNOT proceed.” The way this was accomplished was simply by, similarly to (but not the same as) the classic Choose Your Own Adventure method, having multiple routes through the book, with the ‘page numbers’ being a three digit code generated by the student based on the answers to the questions on the current page. I’ve tried to mock up (from distant memory) the top and bottom sections of a typical page:

In effect, the instructions routed the student back and forth through the book based on the level of understanding demonstrated by answering the questions: a kind of flow chart or algorithm implemented in a paperback book, and with little incentive to ‘cheat’ since it was not obvious how far through the book one was. (Of course, the ‘length’ of the book would differ for different students depending on how well they did in the exercises they did.) There were no answers to look up: proceeding to whatever next stage was appropriate would show the student whether he/she had understood the concept correctly.
When I can find the books again (along with a lot of my old books, I don’t have them with me where I’m living at present), I will certainly post up some real images on the blog, and explain the system further. (It’s frustrating me now as I type this early on a Sunday morning that I can’t remember the name of the publisher: there may well already be an enthusiasts’ website devoted to them. Of course, I can remember the cover design pretty well, with wide sans-serif capital letters on striped blue/white and murky green/white backgrounds; I guess that’s why I’m a designer!)
A weaker way of achieving a ‘mistake-proofing’ effect is to use the output of one page (the result of the calculation) as the input of the next page’s calculation, wherever possible, and confirm it at that point so that the student’s understanding at each stage is either confirmed or shown to be erroneous. So long as the student has to display his/her working, there is little opportunity to ‘cheat’ by turning the page to get the answer. No marks would be awarded for the actual answer; only for the working to reach it, and a student who just cannot understand what’s going wrong with one part of the exercise can go on to the next part with the starting value already known. This would also make marking the exercise much quicker for the teacher, since he or she does not have to follow through the entire working with incorrect values as often happens where a student has got a wrong value very early on in a major series of calculations (I’ve been that student; I had a very patient lecturer once who worked through an 18-side set of my calculations about a belt-driven lawnmower which all had wrong values, based on something I got wrong on the first page.)
Overall, the field of ‘control’ as a way of checking (or assisting) understanding is clearly worth much further consideration. Perhaps there are better ways of recognising users’ blind spots and helping resolve them before problems occur which depend on that knowledge. I’m sure I’ll have more to say too, at a later point, on the issue of widespread ignorance of certain subjects, and gaps in understanding and their effects; it would be interesting to hear readers’ thoughts, though.
Footnote: Security comparison
We saw earlier that there seems to be little point in educational software limiting the number of guesses a student can have at the answer, at least when the student isn’t allowed to proceed until the correct answer is entered. I’m not saying any credit should be awarded for simply guessing (it probably shouldn’t), just that deliberately restricting progress isn’t usually desirable in education. But it is in security: indeed that’s what most password and PIN implementations use. Regular readers of the blog will know that the work of security researchers such as Bruce Schneier, Ross Anderson, Ed Felten and Alex Halderman is frequently mentioned, often in relation to digital rights management, but looking at forcing functions in an educational context also shows how relevant security research is to other areas of design. Security techniques say “don’t let that happen until this has happened”; so do many architectures of control.